Cp\Cpk\Pp\Ppk\Cpm\Cpmk\Ppm\Ppmk\cm\cmk的全面总结

sontime

  j2 `" N4 T: a谈到过程能力，首先得解释变异（或者叫波动），正是因为有了变异的存在，才出现了能力大小。产生变异的原因可以归结为两种，一种是普通原因，一种是特殊的原因。
所谓的普通原因就是平时一直客观存在，对过程有一定的影响但不明显，而特殊因素则是偶然出现，对过程影响很大。举例说明：在一个有空调的房间进行培训时，虽然空调可能是设定在25度，但由于房间内外温度存在差异，所以每时每刻都会有能量在和房间外进行交换，所以如果用足够精确的温度计测量房间的温度就会发现房间里的温度其实并不是恒定在25.000度，而是24.99,24.98,25.00,25.01…..在微小的在一定范围内进行变化，这时我们就说受到的是普通因素的影响，而如果有人推门进来，那么在这瞬间，房间内的温度会出现较大变化，此时我们说受到了普通因素和特殊因素两种影响。
过程只受普通因素影响的时候在控制图上表现为过程是受控的，如果有特殊原因的影响在控制图上会有异常点的出现。
所以我们如果用Cp和Cpk来衡量过程能力，前提是要过程稳定且数据是正态分布，而且数据应该在25组以上（建议最少不要低于20组，数据组越少采信结果的风险越大），也就是说计算Cp,Cpk只考虑过程受普通因素的影响。计算公式为：Cp=(usl-lsl)/6σ;1、Cpk=(1-k)Cp;k=|u-M|/(usl-lsl)/2;2、Cpk=min{(usl-u)/3σ ,(u-lsl)/3σ };注释：usl为上规格线，lsl为下规格线，u为实际测得的平均值，M为上下规格的中心点，K值表示的意思是实际平均值偏离中心值的程度，此时的 即为只考虑普通因素产生的变异，通常根据控制图的不同采用Rbar/d2,或者Sbar/C4,在minitab里有三种不同的估算方法。
Pp,Ppk的计算公式和对应的Cp,Cpk计算公式相同，所不同的就是分母部分的变差不同，在此时变差是用标准偏差的计算公式进行计算的，此时的变差包含了普通因素和特殊因素产生的两种变差，也即在同一个过程下，此变差应该大于等于上面计算Cp,Cpk只考虑普通因素时的变差，当且仅当此过程只受普通因素变差影响时，两者相等，此时Ppk=Cpk，所以说理论上Cpk应该是恒大于Ppk,但很多时候在minitab中计算出的Ppk会略微大于Cpk，这时因为Cpk的变差是估算得来的，所以会有一定的误差，但并不影响对最终过程能力大小的评价。
6 h$ I0 m1 y# {' z* h' R3 p& ]因为过程只受到普通因素变差影响是理想状态下的，从长期来说过程总会受到各种特殊因素的影响，所以说Cp\Cpk又被称为短期过程能力，也叫潜在过程能力，Pp\Ppk又叫长期过程能力，也叫性能指数。另外因为Pp\Ppk的计算不需要过程稳定（因为在计算公式中已经考虑了普通和特殊两种因素的影响），所以在PPPAP手册中要求在产品进行试生产过程不稳定时（此时过程受两种因素影响）用Ppk衡量过程能力，要求Ppk>=1.67才能进入量产阶段，所以又把Ppk 称为初期能力指数。
很多公司由于对过程能力的一知半解，往往只要求计算Cpk的指数来衡量过程能力是否足够，事实上进入正常生产后应该通过Cp\Cpk\Ppk三个指数之间的产别来判断过程是否有问题，如果有问题是管理上还是技术上有问题，根据上面的计算公式，当Cp〉1.33表明过程变差比较小（因为usl-lsl是设计或者客户已经给定的），此时还要看Cpk,当Cp和Cpk相差很大时表明过程有较大的偏移,需要做居中处理，再比较Cpk和Ppk，如果两者相差不大表明受特殊因素的影响小，如果两者相差很大表明受特殊因素的影响很大，特殊因素的影响往往比较容易找到。如果Cp值本身就很小那说明过程受普通因素的变差影响大，此时若想提升过程能力往往更多的投入和更高的决策才能使问题得到解决。所以即使有时候Cpk值很高( 比如大于2 ,如果其与Cp\Ppk相差较大的话还是需要对过程进行改进。
如果Cpk比Ppk 大很多往往一种可能是过程并没有受控，控制图上有异常点的出现，计算人员错用了结论。
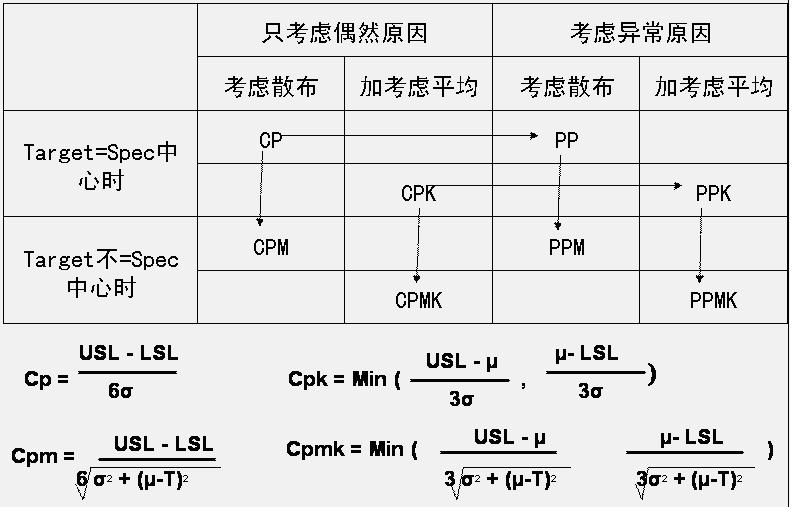
Cpm\Cpmk\Ppm\Ppmk即所谓的第二代能力指数对应的公式和上述对应公式也相同，所不同的还是下面变差部分的不同。
2 d/ Y- X8 v, O7 D8 w- QCp\Cpk\Pp\Ppk默认的是目标值和规格中心重合，而当目标值和规格中心不重合时（比如设计直径为10+0.5-0.5,此时规格中心值为10，目标值也为10，而如果是10+0.5-0.1,则规格中心值变成了10.2,而目标值仍为10）需要用Cpm\Cpmk\Ppm\Ppmk这四个指数，具体的计算公式见图片。
Cm\Cmk是设备能力指数，单纯的用来衡量设备的能力情况，计算公式与Cp\Cpk相同，不同的是在进行样本采集时要求在稳定的过程下固定除设备外的其他条件. CMK取样条件与CPK的区别就是CMK样品要连续取，CPK样品取样有个INTERVAL。

lanszd

不能说是缪文，至少也有2个很重要的说法是错的。为了不再误导大家，我必须说一下正确的观点。

2 ^; m5 N5 }+ Y; s  E' \第一： CPK恒大于PPK?
" F! r$ M& d7 W! i+ y' l+ n3 n如果单单套公式计算的话，也许是这样的.
但是有一个很重要的前提是PPK计算的时候是不分组的，因为这个指数是一次性的，不存在分组的问题。一旦分组的话，结果就会有差异。这就是为什么如果我们非要将一组长期的数据强行计算ppk时，minitab的计算会和和我们套用公式计算时不一样的原因。我们套用公式计算的时候。是N组数据一起求变差σ，而minitab是分組計算。
通过一般对这2个指数的要求也可以知道，我们一般的要求是PPK>1.67,而cpk只要>1.33就算过程稳定了,如果cpk恒大于ppk，为什么不要求cpk>2呢。


  R9 d. y) _. N( J+ V第二，Cp\Cpk又被称为短期过程能力？ 这个必须要澄清
: W& R9 s+ P+ d4 x" HCPK和ppk到底哪个是短期过程能力，这其实争论了很久，很多教材说法也不一样，因为确实在SPC手册上没有说明确。
其实这从PPAP的要求上就可以知道。
PPAP手册上明确要求提交的是初始过程能力，也明确说明要求提交的是ppk，也就是所谓的初始过程能力研究，这才是短期能力指数。因为在PPAP阶段，不存在大量生产的问题，也就没有分组的问题。一旦进入量产，人家要求的就是cpk了。因为cpk考虑了分组之间的差异。
$ z  l* h$ \4 H& `% N" h; E* k通俗的说，1天我记5个数据，但我第2天来，很多参数就已经变化了，设备的温度啊，刀具的磨损啊，原材料也可能换了一批了，经过每日累计的过程，总的变差会很大，cpk反应的正是这样一个长期过程中产品的稳定性。
短期能力ppk 你也许能控制的不错，可是如果你的刀具管理的不好，你的设备保养得不好，你的人员素质差异很大，原材料批和批之间差异很大，就会造成你长期能力cpk不一定很好。所以cpk的要求一般都比ppk要低。



希望我的解释能让大家忘记一些错误的看法。
4 L+ f: a3 X8 n! b: x1 P
: k1 V$ _& Z( _- |* B[ 本帖最后由 lanszd 于 2009-9-16 19:47 编辑 ]

trues2006

20楼的朋友说的有道理，但是我也有几点要说的：
3 P" |; t6 p; Z! Y& Q. A1、CPK与PPK所表达的意义是有区别的，CPK强调的是过程的稳定程度，PPK表达的是过程能力；二者都是针对能力的，不过，CPK是稳定的保证能力，PPK是初期，设备，工艺对该产品开发与生产的能力；支持的是，CPK恒大于PPK，是初学者对公式的理解，没有什么实质的意义；
! |! {- j9 ?& d
2、至于以前一些文献中提到的长期及短期过程能力，现在已经被很多文献删掉了，因为，这个概念对我们研究过程及性能的能力没有实质的意义；
8 T, }6 H+ N* T7 I3 f- i但是，我还是支持，CPK短期过程能力，因为，我们的过程控制能力是根据控制图逐步改进的，如果没有质量改进就没有质量提升的空间，而影响CPK的因素是两个，一个是无法改变的，一个是偶然发生的，偶然发生的会通过我们的过程图识别出来而即刻被改善，则CPK将立即改变，稳定是短期的；而PPK是长期的理解是，改变我们理解为无法改变的那个因素，需要做工艺改进，设计变更，出来的产品类似于新产品，需要长期评价，如果达到了我们的PPK的要求，则，我们的CPK将会得到更进一步的提升；这个过程就如我们做六西格玛改善一样，是循序渐进的过程，确实我们的生产过程发生质地变更的过程；
这是我的理解，不知20楼的朋友是否赞同；

lanszd

原帖由 trues2006 于 2009-9-17 10:18 发表 http://www.3dportal.cn/discuz/images/common/back.gif
) V; a" j( v: t20楼的朋友说的有道理，但是我也有几点要说的：
1、CPK与PPK所表达的意义是有区别的，CPK强调的是过程的稳定程度，PPK表达的是过程能力；二者都是针对能力的，不过，CPK是稳定的保证能力，PPK是初期，设备，工艺对该 ...

不错不错，真理越辩越明
第一点我们的看法应该是一致的
1 m0 S. V% G) h; w第二点我们对指数的含义理解也是一致的。区别的在于对长期和短期的理解。
8 i6 [: ?+ o" v* D5 q; o( t" J我认为的长期和短期指的是搜集数据的时间长短，指数反映的时间段的长短。
1 m. C, E' D* M3 q而你说的长期短期指的是指数本身代表的过程的长短。我觉得你说的应该也是正确的。

Leonard_Lee

22# trues2006
4 ]! k  g; ^- L, L6 F1 MCpk 要求在稳定的前提下才能计算，所以是必须先排除特殊原因的变异的，Cpk只受普通变异的影响。

JackyWu

楼主写的很详细，学习了！

rialto

多谢分享，这个不错！

mml487

学习！！！！！！！！！！！！！！！！！！！

ythfy

学习了，谢谢分享。

jhlafr

这几个指数，目前还存在一定的分歧，重要的是要明白指数代表的意思和所要衡量的内容。

songyang2008

这几个之时的歧义看都说的有道理，有的看理论公式，有的考虑实际应用。不知道哪个是真理！
谁出来做个判定！！！！！

qqkkdok

讲这个课如果要收钱，你们来学吗？学费多少合适？
我觉得楼主的比后面几个道友的要清楚一些。楼主高人啊。。。
: S2 }8 e; E9 J8 r6 ?% k! w后面道友的概念觉得有点问题。
3 |: A8 r8 @5 g9 o# mCPK是分析什么的？
PPK是分析什么的？
我觉得要知道到底要分析什么问题，才会去想要算CPK，还是PPK。

nanfeng36

谢谢分享。