|
|
发表于 2007-3-9 14:41:30
|
显示全部楼层
来自： 中国辽宁营口
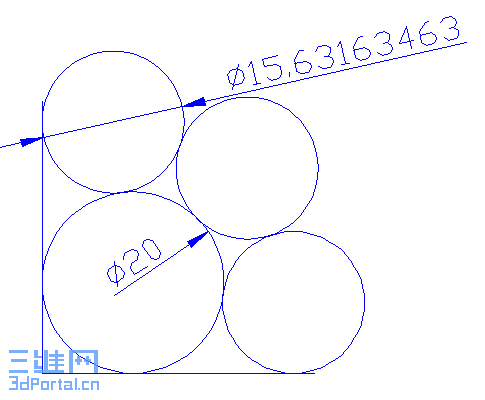
用VBA画图方法
VBA源代码：
! B$ r/ d4 i X1 g, D/ ^ [* U; R
; e8 M5 A# T, P+ Q$ B% D" ]Sub A() '本程序以20圆的圆心为坐标原点
) R% }. y$ K+ o- e' g$ t. r Dim Y As Double '左上方小圆圆心纵坐标
$ s- `% q9 @1 f Dim Y1 As Double, Y2 As Double, B As Double, B1 As Double '迭代运算中间变量" }; K0 E; V0 I' M( }3 p# g" [
Dim R As Double '小圆半径
[. O* P! |) v" Y/ y* Q- `0 H Dim O(2) As Double '坐标原点7 |' G0 L' ^( i1 y3 I+ X4 K# w9 n
Dim O1(2) As Double '左上方小圆圆心7 V2 n$ ?$ \: w% d) M8 A1 x
Dim O2(2) As Double '右上方小圆圆心% y$ Z4 r) H7 h5 c
Dim O3(2) As Double '右下方小圆圆心1 m' u& B8 q. ?2 k* d' I
Dim P1(2) As Double, P2(2) As Double, P3(2) As Double '直线起端点
z5 T# R' @8 i Y1 = 10 '迭代运算边界条件9 E% n4 T% h& f* d" c
Y2 = 203 ?( w+ }' `+ ]' J% I
Do '计算合适的小圆圆心纵坐标
6 y; ]; J! y% Y% w7 k& @+ w Y = (Y1 + Y2) / 2( ]( p1 @* _# F; I$ H" ~
B = -(2 + Sqr(2)) * Y ^ 4 - 40 * Sqr(2) * Y ^ 3 + 1600 * Y ^ 2 - 16000 * Sqr(2) * Y + 320000 + 160000 * Sqr(2)
8 I k$ ]5 ^4 q {( R3 V If B = 0 Then
8 J% @: \, q/ E" F Exit Do9 S+ [3 @+ n1 w! A2 O$ w* j
ElseIf Y = Y1 Then, W8 S7 V$ \! Y6 Y( {5 ?
B1 = -(2 + Sqr(2)) * Y2 ^ 4 - 40 * Sqr(2) * Y2 ^ 3 + 1600 * Y2 ^ 2 - 16000 * Sqr(2) * Y2 + 320000 + 160000 * Sqr(2)& G$ y2 x: [* J4 T# c
If Abs(B1) < Abs(B) Then Y = Y2
/ N( x: Q& E3 O d" c2 H Exit Do
# a! W! p8 ]5 } ElseIf Y = Y2 Then
* U! f! Z9 T* f9 R$ X- P" p* s1 M B1 = -(2 + Sqr(2)) * Y1 ^ 4 - 40 * Sqr(2) * Y1 ^ 3 + 1600 * Y1 ^ 2 - 16000 * Sqr(2) * Y1 + 320000 + 160000 * Sqr(2)
* r1 @5 \/ z) i8 k" g9 a3 p/ F If Abs(B1) < Abs(B) Then Y = Y1+ A9 N( F0 x/ l3 ^( |
Exit Do
/ W9 K" G) Z7 M% T, F1 a9 O ElseIf B > 0 Then- i4 ^+ W+ a2 x5 ?/ x* b1 T
Y1 = Y @0 @+ n7 P; u
Else
- O$ \, K8 X+ D, v' ^ Y2 = Y, a2 }3 \( q' }7 H& Z
End If6 Y |4 f @! x: O
Loop5 T( Z* J0 g. Q5 `4 m: a
R = Y ^ 2 / 40 '小圆半径, i0 w. K9 A/ \' o. C% ?& H! c
O1(0) = R - 102 P% w4 b/ T4 c) V( w$ ^$ b, T) d
O1(1) = Y '各点赋值+ X( \5 h. u7 l7 y
O2(0) = Sqr(0.5) * (10 + R)( C* ~+ q) N# a4 I. `6 r% T
O2(1) = O2(0)# y9 V3 M$ y" Y4 |
O3(0) = O1(1)
3 ]- A" A0 f9 C( R. n3 w O3(1) = O1(0)
8 _& k( N) O q8 k w6 j P1(0) = -10! j$ i K& h% `/ E& e0 c5 N+ _. Z
P1(1) = -10 r4 v7 y% N' u
P2(0) = -10
9 p2 ~* |' J" a; _ P2(1) = 20( \1 M& s3 _; K4 ^6 [8 E
P3(0) = 20. w, m% k5 l9 T5 W$ D
P3(1) = -10& t7 ` f6 r6 r' r" n
With ThisDrawing+ Z, H- ~3 p: P8 \0 k' d8 _
.ModelSpace.AddLine P1, P2 '画直线
, A3 K9 z$ k! B* J. j5 a. K1 }8 v .ModelSpace.AddLine P1, P3; R% ?0 Z; p S" `
.ModelSpace.AddCircle O, 10 '画大圆
6 C' f2 s) E8 _ f .ModelSpace.AddCircle O1, R '画三个小圆, j. Y6 X( O7 p. ]
.ModelSpace.AddCircle O2, R
6 u* m* f" v1 M* J: v .ModelSpace.AddCircle O3, R
+ b) h6 A; C0 r. F% a End With/ n5 v0 y) [5 s' u5 ?
End Sub |
-
评分
-
查看全部评分
|
发表于 2007-3-9 09:43:24
发表于 2007-3-9 12:21:41
楼主
都好厉害，我没想到的都给想到了／
:L