|
|
发表于 2007-5-20 16:09:50
|
显示全部楼层
来自： 中国
1、求做平面上任意四个圆的外公切圆，在理论上不成立（这与座标系和计算方法无关）；2 l$ c6 E5 Y Q: Y
2、对平面上任意四个圆，可以求解和绘制这样的圆：其圆周分别与四个圆的圆周有相等的最小距离。但对平面上任意四个圆，求解一个圆：其圆周与四个圆圆周的最小距离均小于给定值，在理论上不成立（同样与座标系、算法和是否使用计算机无关）； H+ g% W% s9 {# H
3、对于本命题，四个圆外侧的包络线不是圆。
/ P% H1 ~* t' n; ^" F& d: E; \ 在工程应用中，用连续的、相切的不同半径的圆弧和直线段在合理的精度范围内近似地表述某种曲线，是很常用的方法（这不是巧合）,这在教学和实践（特别是手工制图）中经常可以见到（如用若干段圆弧近似地画出椭圆或一段渐开线等）。在数字技术得到广泛应用的今天，这种方法正在部分地被精确计算、制图并配合数控加工所取代。
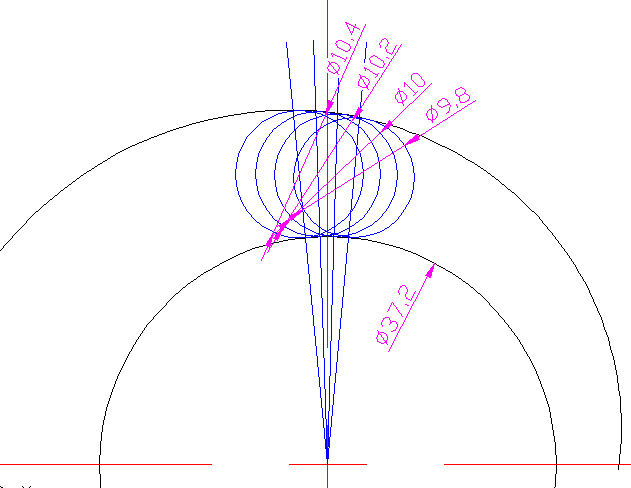
" o/ [4 P7 ^8 H' |/ \ 综上所述，对于本命题，笔者认为：用计算机精确地计算并绘制出四个圆外侧的包络线具有更为实际的意义。以下为笔者在AutoCAD上用VBA编制的包络线计算和绘制程序（由于命题中未明确给出小圆圆心轨迹的数学模型，笔者根据命题已有的条件假设小圆圆心轨迹为阿基米德螺线）
) O6 s3 y0 ?) A( v0 {6 g; J$ X- ~$ p7 p2 U! c S/ o
# P2 o- B$ b. `. i
Sub QX()/ ]( U1 i! t; [) o$ H- W
Dim R As Double, A As Double, B As Double, Theta0 As Double, R0 As Double
) j. R( f6 H# g7 |6 {5 q Dim Theta As Double, I As Integer, P() As Double, T1(2) As Double, T2(2) As Double
- W" j7 z4 n# U7 T8 j Dim O As Variant+ T% Z" V' z, E/ g3 [
6 E) h$ v+ i/ @6 G R = 18.6 '内切圆半径18.6# S8 E" o& ^. |" y, l# [( u+ U
A = 5# / 3.14159265358979 '小圆绕内切圆旋转每180度半径增大5
8 I3 w; l1 V/ S9 S Theta0 = 88.4 * 3.14159265358979 / 180# '小圆在内切圆88.4度方向时半径为53 z7 p: D2 F3 O( x$ y" H5 `
R0 = 5#
9 Q' b* U& _$ l$ P7 U7 }0 q With ThisDrawing& b# Q# P# D- s! C; c4 n
O = .Utility.GetPoint(, vbCrLf & "指定内切圆的圆心位置：")
! r$ X& F4 X: B7 W( Y6 I Do Until Theta > 3.14159265358979 * 2 '计算小圆从0度角起绕内切圆360度的包络线轨迹，每间隔1度计算一个点的座标/ u" A' k, J" f3 T/ k# k4 }5 }% G/ Y
Theta = 3.14159265358979 / 180# * CDbl(I); ~& m( E8 Y: d! ?; {- E* o
B = A * Theta + R + R0 - A * Theta0& |1 B7 T. q& u, `, T& J: m
If A * Cos(Theta) - B * Sin(Theta) <> 0 Then+ n; m/ Q; M' E+ Y6 k, Z& g
ReDim Preserve P(I * 3 + 2)
K, V |0 p3 H9 M$ Y If A * Cos(Theta) - B * Sin(Theta) > 0 Then
& ?; M6 Z9 F( i P(I * 3 + 1) = (A * R * (B * Cos(Theta) + A * Sin(Theta)) _; A# H" a2 B z
+ B ^ 2 * (B * Sin(Theta) - A * Cos(Theta)) _! Q8 U0 F: N) H
- Sqr((A * R * (B * Cos(Theta) + A * Sin(Theta)) _6 h3 f% g) y ~& }0 |6 L
+ B ^ 2 * (B * Sin(Theta) - A * Cos(Theta))) ^ 2 _! z$ T& O, P; D
- (A ^ 2 + B ^ 2) * (A ^ 2 * R ^ 2 - 2 * A * B * R * Cos(Theta) * (A * Cos(Theta) - B * Sin(Theta)) _
& N9 q7 ] Z; m% \$ N* x + (2 * B * R - R ^ 2) * (A * Cos(Theta) - B * Sin(Theta)) ^ 2))) / (A ^ 2 + B ^ 2); l: J/ G, I/ {. s
Else5 @5 }- z' n% @/ @; G5 ?3 A) |
P(I * 3 + 1) = (A * R * (B * Cos(Theta) + A * Sin(Theta)) _9 y0 _* V* |* r+ V/ a* H
+ B ^ 2 * (B * Sin(Theta) - A * Cos(Theta)) _% _) Z$ z1 E" T4 |" x
+ Sqr((A * R * (B * Cos(Theta) + A * Sin(Theta)) _" C! |/ `, [8 O1 i$ j6 C' c: o
+ B ^ 2 * (B * Sin(Theta) - A * Cos(Theta))) ^ 2 _
: |( u- _; c& m4 F3 e+ D- W - (A ^ 2 + B ^ 2) * (A ^ 2 * R ^ 2 - 2 * A * B * R * Cos(Theta) * (A * Cos(Theta) - B * Sin(Theta)) _
2 |& U+ A8 p2 P8 t5 v$ E + (2 * B * R - R ^ 2) * (A * Cos(Theta) - B * Sin(Theta)) ^ 2))) / (A ^ 2 + B ^ 2)
1 C! E, D6 l2 s: b! X End If2 m6 }6 }' [% a1 g, [
P(I * 3) = (A * R - (A * Sin(Theta) + B * Cos(Theta)) * P(I * 3 + 1)) / (A * Cos(Theta) - B * Sin(Theta)) + O(0)# k+ [+ P" H3 o
P(I * 3 + 1) = P(I * 3 + 1) + O(1): |, P' W3 Q1 F2 f0 c6 x' z' Y5 K
I = I + 1
. H r; X6 |. F& L End If
, \- G# o( Y x' y* N+ | Loop
4 H4 z+ X: T# ], q) z/ M3 E .ModelSpace.AddCircle O, R '画内切圆
, U& v. p7 F% d3 U' O o+ X .ModelSpace.AddSpline P, T1, T2 '画包络线" d, E0 Q- y6 W9 e9 t3 h
End With9 S9 t2 ~. A9 R# G
End Sub5 C) ]$ y4 A! \) v: W
1 J6 P% A7 K' G' u. W
9 c1 o' r) ?; k6 G4 I6 Q' a5 x: v, K' z: ?3 u
[ 本帖最后由 woaishuijia 于 2007-5-20 16:22 编辑 ] |
-
-
QX.rar
60.6 KB, 下载次数: 24
QX.dvb 主要演算过程.doc
评分
-
查看全部评分
|
发表于 2007-5-8 15:32:57
发表于 2007-5-9 08:57:22
发表于 2007-5-9 14:00:41
楼主
( w/ x$ Y! b# \! J L1 P- W
