|
|

楼主 |
发表于 2009-5-28 22:59:15
|
显示全部楼层
来自: 中国辽宁大连
依次建模
, X' `) b' F6 T1 o' r
9 P8 t2 R, n! \" w. S6 p关键:第二个草绘圆的位置确定: _1 a! r" C" T, M0 [& O
在图三中的点为四环外接正四面体的的重心位置4 b; a" B% w4 E) o
+ X4 | U) d- u, x
参考:
% C- |( a+ Z8 g正四面体就是由四个全等正三角形围成的空间封闭图形。它有6条棱,4个顶点。正四面体是最简单的正多面体。当其棱长为a时,其体积等于(√2/12)a^3,表面积等于√3*a^2。4 h: N7 b0 l( [& A z8 N
: S; J1 C6 D1 C- w4 `4 ~9 w
正四面体是一种柏拉图多面体,正四面体与自身对偶.
" A ~' k& [/ |3 Y正四面体的重心,四条高的交点,外接球内切球球心共点.正四面体有一个在其内部的内切球和七个旁切球与四个面相切,其中有三个旁切球球心在无穷远处.
+ _0 m' o+ }1 k, c& N正四面体有四条三重旋转对称轴,六个对称面.
4 W! a2 P, P0 _' z# @正四面体可与正八面体填满空间,在一点周围有八个正四面体和六个正八面体.' @/ O* B! t" Z
: k5 E( S7 z) [顶点数:4 (相同) 棱数:6 (等长) 面:4 (全等正三角形)! r$ L+ G l( ~5 J
棱长为1时,
$ D+ E/ x s: o5 e高:6^0.5/3,中心把高分为1:3两部分.两条高夹角为2*asin(6^0.5/3)=2*acos(3^0.5/3)=2*atan(2^0.5)=2*acot(2^0.5/2)≈1.91063 32362 49(弧度)或109°28′16″39428 41664 889.这一数值与三维空间中求最小面有关,也是蜂巢底菱形的钝角的角度.
8 s2 J' `9 a- H2 d/ w9 ?表面积:3^0.5$ I) c% M0 v. x
体积:2^0.5/128 h% n) _( ^2 J7 C$ b6 G8 \- K. L
外接球半径:6^0.5/4,正四面体体积占外接球体积的2*3^0.5/9*π约12.2517532%- _' O8 R. v# D& Z
内切球半径:6^0.5/12,内切球体积占正四面体体积的π*3^0.5/18约30.2299894%
: Q+ J+ E0 x, G9 q9 h" W5 E两个面夹角:2*asin(3^0.5/3)=2*acos(6^0.5/3)=2*atan(2^0.5/2)=2*acot(2^0.5)≈1.23095 94173 4077(弧度)或70°31′43″60571 58335 1107,与两条高夹角数值上互补. |
-
1、旋转截面

-
旋转实体环

-
2、草绘曲线
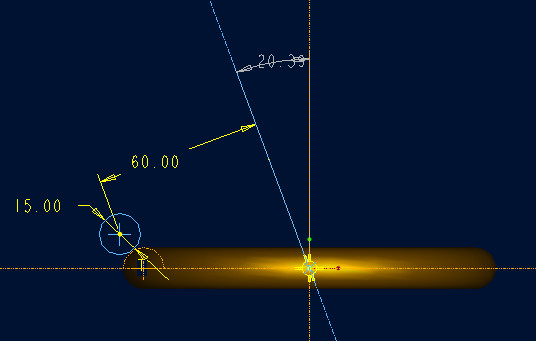
-
3、草绘截面
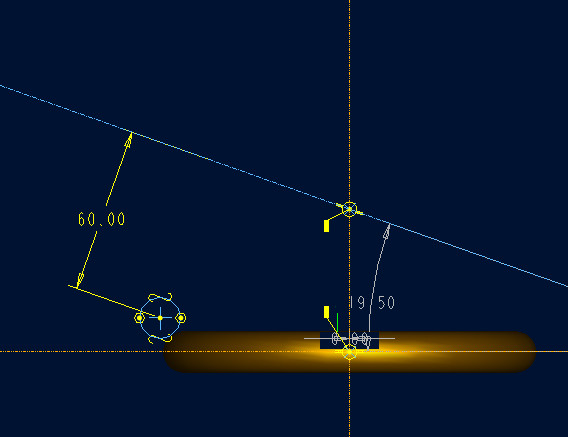
-
4、旋转第二个环

-
5、轴阵列其余两个环

-
6、完成图

|