|
|
 发表于 2014-3-5 16:20:11
|
显示全部楼层
发表于 2014-3-5 16:20:11
|
显示全部楼层
来自: 中国辽宁抚顺
2 r+ h/ W4 d2 F; o
# Z, F9 r3 O7 A* E$ y7 [
7 ?3 k# q+ [* U: Z3 U, X) j
! _9 k0 a3 T3 e) ]
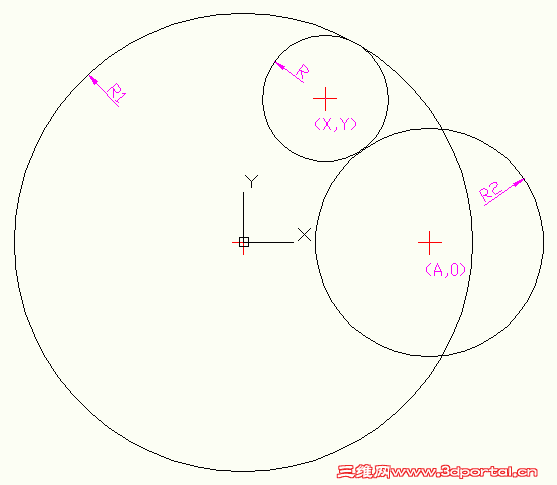
" |% Q1 V8 g) G根据上图可列方程组( L" T" v0 m9 N* m- K& o: @4 C! ~
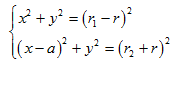
, ?$ B# o- m/ ]5 A' S; N% G联解方程组,消去R,可得动圆轨迹2 r% {; h% \# S! N
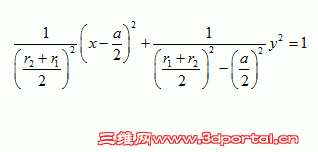
: r2 c& g/ A4 |) i- o) E由上式可知,当两定圆圆心距小于两定圆半径之和时,即两定圆内含或相交时,动圆圆心轨迹为椭圆,椭圆中心位于两定圆圆心连线的中点,长轴半径为两定圆半径的平均值,短轴半径为两定圆半径的平均值的平方与两定圆圆心距的一半的平方之差的平方根;当两定圆圆心距大于两定圆半径之和时,即两定圆相离时,动圆圆心轨迹为双曲线...... |
评分
-
查看全部评分
|