CAD几何作图竞赛题（2017年5月），竞赛结果已公布

sihouko

) j! Y8 d6 U" x7 E. R1 a

大隐于市 发表于 2017-5-24 09:35
9 d/ ?4 [" x' h$ t9 i这一期的题目从答案来看，分歧很大，如果能加条水平线，可能会更严谨一些。
  x. M5 D" l% o( D4 G2 i不过我觉得观察还是得仔细，题 ...

$ g' M7 e1 i4 v! O# b' U21.3534是約束交點重合，正確答案是約束4點（2圓心，2交點）共綫，都可以得到完美草圖。
: P) F, H9 {2 r
以下回答純屬猜測。。
衹要4點共綫，就能得出正確答案。。但是我始終不理解爲什麽會4點共綫。（絕對不共綫就得不到這個形狀的理由）

oxm44

隐藏的条件分析见下图：

7 x8 f4 {% X5 I0 L( Z

* g; y' I; H; S& s  k" U几何作法：

3 I/ }( [. F/ K4 J& R/ @* W

大隐于市

oxm44 发表于 2017-5-24 10:28
3 S- Y* g4 k& O隐藏的条件分析见下图：

感觉没那么复杂，只要确定了P、Q两点在水平线上，直接用偏移命令就可以做了吧。
" J6 W, {2 e- i2 g; E$ g
! [# b% W7 |) J没办法上传大附件，gif有点快，凑合着看。
% i8 I* ?/ @8 o. m0 b6 p9 O; o' A- L

oxm44

这样也可：

大隐于市

oxm44 发表于 2017-5-24 11:21
- l; S, ]3 J/ Q# g$ r' A+ Q这样也可：

" A% V0 Q" U2 r" `# Goxm44老师，你的解法有点问题，从原题中是看不出下面这个条件的：
这里为什么必须要17.5？
比如我随便按22的尺寸偏移，就会得出下面这个尺寸来。
! N# j; K% X' m$ L3 s
8 P' d  m  g! @- T好像没有哪里不符合你的原图吧？
; B+ l! Y" N; d. c. ~

oxm44

大隐于市 发表于 2017-5-24 12:31
. D- g9 F% Q) {) Moxm44老师，你的解法有点问题，从原题中是看不出下面这个条件的：
2 s8 G" C  ]  `8 ~. z这里为什么必须要17.5？
( N6 }; U. P  `+ K% I比如我随便 ...

! o' X6 `" i# J  f+ ], B  O, L' ?
$ g1 K, F5 Y$ O5 ~
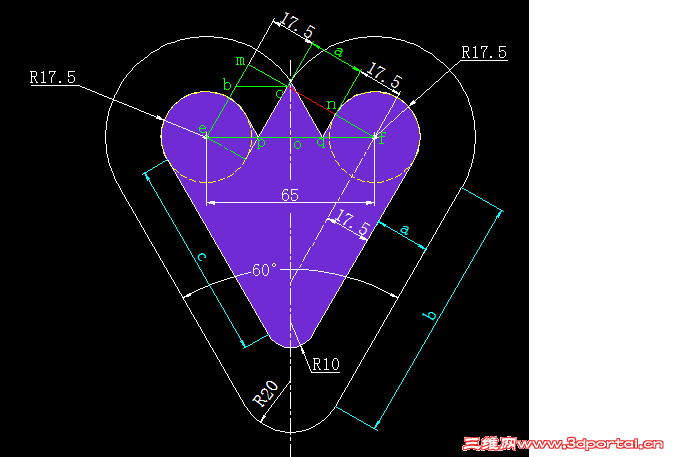
, M, v9 v1 b/ m; N' F9 d图形的对称性可知：ep=qf，故有△mbc与△nqf全等，于是有mc=nf=17.5!

0 d& l1 X5 S9 d' ?. _8 t3 r3 c( o$ M任取a值太无理了！
2 T, |% g" N* |9 a, {+ a. n) R

TKG-09

隐含条件只能猜测，如果划出四点共线，则不会有歧义。我作了两套图，纠结了很久才决定猜猜看。

sihouko

oxm44 发表于 2017-5-24 19:31
- y+ {  h% w/ J5 n3 D4 _图形的对称性可知：ep=qf，故有△mbc与△nqf全等，于是有mc=nf=17.5!
7 a9 ]$ C5 d; p8 Z
任取a值太无理了！

$ _# a( v$ f6 f老師，如果當初條件有明確標明全等的話，確實沒有問題。
但此題abcd4個條件是需要求解的，
所以當三角形mbc與三角形nqf相似or全等即可得到類似的圖形。
但是全等確定唯一解，
* w* h% d/ |$ q1 u/ t單純從題目的表述來看比起以往貌似少了一點嚴謹。
- C, p' @3 T. l/ h$ v# T

大隐于市

如果不强调P、Q与两圆心共线的话，△mbc与△nqf不全等，连相似都不是。
" u" h# V  H+ y! g

oxm44

大隐于市 发表于 2017-5-25 09:52
9 p5 o" @0 n2 C如果不强调P、Q与两圆心共线的话，△mbc与△nqf不全等，连相似都不是。

& c0 n7 N, n: s0 g( P8 f注意，此p、q，并非彼P、Q！p是由c所引大圆的切线与两圆心连线ef的交点，q是由n所引小圆的切线与ef的交点！怎么能不与ef共线？
% I$ o  V8 x* }6 v# M2 r你这个歪理图有点可爱！
! J1 @  ?  a' Z1 v
3 Z& A' k# d! C( ]

13430599092

这题不算难啊，主要就是切线的旋转角度啊，要不要我给你们来几道题？

lisc2000

这个题破定太多
* O. ~+ S  I) j, f8 {不仔细标注，中间的尖角就是一个60度的角，而看不出来是两个弧相交
出题时候应该注释这个尖角
& ^! A+ L+ s, ]6 \7 _所以这个应该每个人都给补偿10个三维币做精力损失费

lisc2000

图片自设15尺寸也可以做出上图
. i6 u% g, }! t0 ^9 H; D这个可有错误？
  X1 l; b7 J1 g* u& G% [6 n