|
|
马上注册,结识高手,享用更多资源,轻松玩转三维网社区。
您需要 登录 才可以下载或查看,没有帐号?注册

x
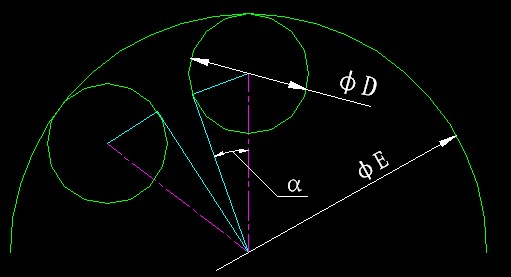
如图所示。" y0 {" J, Q+ r( R. l
E:内滚道直径;D:滚子直径;Z:滚子个数;T:圆周总游隙9 e5 q) A% h$ X+ `
根据INA轴承手册: T=Z*(E-D)*sin(180/Z)-Z*D -------式1
0 C2 W9 l& i; q: r根据NSK轴承手册: T=π*(E-D)-π*D/sin(180/Z) ------式2
: H6 ^5 z$ X$ O9 p两者计算出来的圆周总游隙T相差0.002~0.03
# O7 P$ A5 Y/ C我不知道哪个更准确,就自己推导了一下,得出:
+ F+ B/ S. O5 F V% Wsinα=D/(E-D)+ B3 y8 {) T& `4 H- k: l
T=sin(z*α)*cosα*(E-D) -----------式3! Z k7 n! P* J- x @7 G
计算出来,跟INA的相差0.00001~0.0009
) ], F9 I( f4 V2 n应该可以排除计算精度的可能,那么,为什么有万分之几的差别?
- l8 W* `5 L6 _2 x当滚子数较少时,差别较大,滚子数目越多,就几乎没差别了。1 E- w/ @5 Z" W4 R H) T+ Q
各位高手,帮我推导一下。( P0 I( t* ]3 o# y! t' R
' R' H+ ?- q7 b6 G4 Q8 o4 h; e. k
|
|