又来求助了，求大大解救

明天你好吗

不规则四边形（即没有一对边是平行的），怎么求最大内切椭圆。
我的思路是求椭圆心和切点，但是不知道求？可否用透仿作出来？
4 b+ D: r" y5 p$ ]. m4 `( Y

明天你好吗

不知为何，我用透视法作图出来不符合。
中心透视虽然面积比是变化的，但是两个图比较的话，正方形的内切圆面积是最大的，透视以后占的四边形面积比也是最大的吧？
& k2 h/ M3 H. S我发现将不规则四边形改为梯形（即有一对边平行）的话，原理就变为一点透视（灭点为Z轴），最终得出的切点和透视以后四边形最大面积的椭圆切点是同一的。
: u( G% V' c' \6 n请指教？
6 d( B+ w- a- n4 M7 s8 J* h
* }6 R7 k: n+ f: L8 ^% G9 S- Z下面是约束后的可能最大面积
" H7 w+ `9 c$ R$ ^6 y

woaishuijia

2 `  H2 V5 A1 p6 x9 T

明天你好吗 发表于 2016-1-26 15:14
5 }! f" f: [0 T中心透视虽然面积比是变化的，但是两个图比较的话，正方形的内切圆面积是最大的，透视以后占的四边形面积比也是最大的吧？

正因为中心透视面积比是变化的，两个面积就没有直接的关系了。

明天你好吗

woaishuijia 发表于 2016-1-26 22:42
正因为中心透视面积比是变化的，两个面积就没有直接的关系了。

2 ]4 y* C5 }/ \0 p& `7 m2 x% v, |3 y从其它思路不知能不能作？

woaishuijia

几何画法没戏。参数约束也未必保证椭圆面积最大

chenmik

我在贴吧里看到过类似的一个帖子，但没看明白，楼主有兴趣的话可去看下，如果知道发解法的话，也希望楼主给大家分享一下。
, v9 `, F8 r' U3 X& ]  x. thttp://tieba.baidu.com/p/4318600719

明天你好吗

, n$ X- Y. k4 Z0 `# \

chenmik 发表于 2016-1-28 11:18
我在贴吧里看到过类似的一个帖子，但没看明白，楼主有兴趣的话可去看下，如果知道发解法的话，也希望楼主给 ...

梯形可以看成是有内切圆的等腰梯形透视仿射，那么该圆面积比/例最大，且切点线平行与底，又过对角线的交点
- Z5 q7 Y! h0 V据仿射的同素性平行性可知该梯形的四个切点位置。最后变成四点作椭圆了
6 e! v0 X' O2 e& P, [1 k
+ R4 ?" b; K: u' x  O


- {* X' U* w5 T3 m& x

明天你好吗

woaishuijia 发表于 2016-1-28 05:45
& h3 ^9 s0 @- a  ]. R8 \) i几何画法没戏。参数约束也未必保证椭圆面积最大

版主大大，如果是一般梯形仿射为具有内切圆的等腰梯形的话，具体的怎么仿射？透视轴是哪条，透视方向是哪个方向，比如对应点的连线就是方向。我只知道结果是这样，怎么仿的过程不清楚
4 d7 j" _7 M: A5 h  t2 F( B

woaishuijia

% q' P% G5 j5 c5 \

明天你好吗 发表于 2016-1-28 19:03
版主大大，如果是一般梯形仿射为具有内切圆的等腰梯形的话，具体的怎么仿射？透视轴是哪条，透视方向是哪 ...

. n: S* R7 v, ]/ t+ [" ^6 U我的思路和你有点小区别,我是把梯形及其内切最大面积椭圆看作是一个矩形及其内切最大面积椭圆的仿射.
因此,梯形内切最大面积椭圆的中心就在上下底中点连线的中点,与上下底的切点就是上下底的中点,与两腰的切点就是原始矩形两垂边中点在仿射梯形两腰的对应位置,且这两个切点与梯形底边的距离是相等的.
于是只剩下一件事,在梯形的腰上找出原始矩形垂边中点的对应位置.
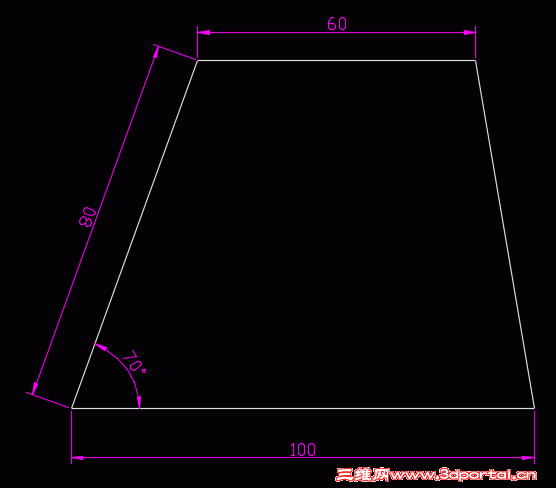
我按照@chenmik 在6楼提供的链接画出了梯形
! M9 e5 e& S0 ^! [  ^
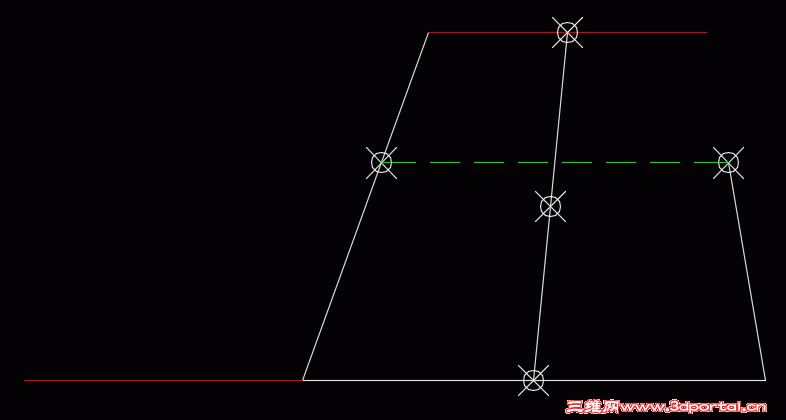
以梯形右上角为基点,复制上底到梯形的左下角,参照缩放梯形右腰,基点为梯形右下角,参照长底为上下底长度之和,新长度为下底长度
; }4 I1 f# h# T3 {  R
$ U2 [9 T5 f. R% T. D/ t梯形内切最大面积椭圆的中心点,与四个边的切点都在这里
/ s. n0 K( v* H2 y$ I* a" z
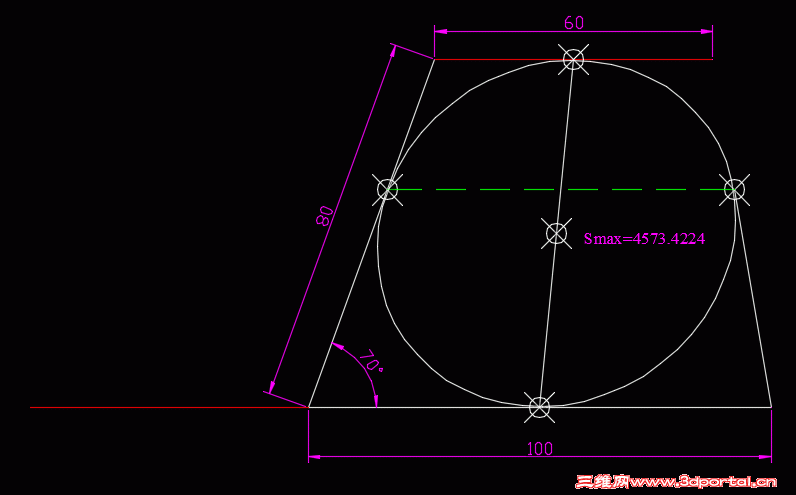
画出的结果与那个帖子的结果是一样的


- O3 L- ?$ e5 M: t

woaishuijia

明天你好吗 发表于 2016-1-28 19:03
6 m# n6 N$ E9 V  |" l0 F版主大大，如果是一般梯形仿射为具有内切圆的等腰梯形的话，具体的怎么仿射？透视轴是哪条，透视方向是哪 ...

回到你的问题上来,按照你的思路,我是这样做的
0 ^% z8 u0 K' V* Y. }- e先画和上帖一样的梯形

以下底中点为第一点,向上两点画圆,直径大于80,小于100.(事实上,圆的直径取多大--只要不等于梯形下底长度--都不影响画图,但取80到100之间可以使画出的有内切圆的等腰梯形的上底比下底短且比上图的梯形上底长.更便于直观上的理解.),画出该圆的外切等腰梯形,该等腰梯形与上图梯形共有下底.顺便把上图梯形两个底边中点连线画出来.

由等腰梯形左上角到下底的垂足(图上绿色直线的下端)向图1梯形左上角连线(图中青色直线)
+ |' a9 e2 k* J+ r& l. m6 N
分别延伸青色直线和图1两底边中点连线(黄色)使二者交于一点,这就是灭点
+ O& t2 h" v! m
由等腰梯形内切圆与左腰的切点到下底的垂足向灭点连线(图上红色直线),该直线与图1梯形左腰交于一点,这就是要求的切点
& {+ T$ q) N+ t) i1 Q

明天你好吗

woaishuijia 发表于 2016-1-29 13:57
, U2 Z2 @( T- x' C2 _- V9 \2 i回到你的问题上来,按照你的思路,我是这样做的
先画和上帖一样的梯形

谢谢版主，中心透视是在用仿射作图过程，却无从下手的情况下而尝试的方法，发现一点透视和仿射一样，/两点，三点透视就不一样/。我没表达清楚，仿射的视点是在无穷远处的，所以方向是平行线，而中心透视视点是有距离的，不一样.
  @% }* `  q( Z3 v* h. ~请看下图，我想要统一的解法，三角形，平行四边形都能用仿射作，关键是找到透视方向，和透视轴，怎么在有内切圆等腰梯形的情况下作一组仿射

( p7 _9 q0 T4 u' z; }平行四边形也一样
) [: m% L1 _7 f7 Y- |

' i9 {9 K* O4 e- w0 B9 H

明天你好吗

再上一下，对帖子题目的/另一种解法

明天你好吗

7 C6 K' l4 i! B' Q

woaishuijia 发表于 2016-1-29 13:57
, }/ ?# b1 P* F# F9 _; Q1 Z0 u! i* |- E回到你的问题上来,按照你的思路,我是这样做的
4 B) e0 R$ S; [0 R先画和上帖一样的梯形

" C- y. d! V( C这个灭点，应该用/了4点共线和等腰梯形中点线垂直于基线，画面是垂直的，灭点为在y轴。学习/了

woaishuijia

明天你好吗 发表于 2016-1-29 18:00
这个灭点，应该用/了4点共线和等腰梯形中点线垂直于基线，画面是垂直的，灭点为在y轴。学习/了

. k) G" X/ @/ Z" b9 h) N
9 D) ?  \5 n5 s8 a7 Y- R你是这个意思吗？
! z( C3 V+ b: P8 G) f, O: w- K

明天你好吗

woaishuijia 发表于 2016-1-29 18:53
) P9 x0 j5 N2 v5 s1 h* |你是这个意思吗？

& y  U. [8 U9 M+ M' p( E对，是这个。版主大大能否给出具体步骤？？？

woaishuijia

明天你好吗 发表于 2016-1-29 19:09
" N. ]3 R7 X: L2 @& ^, j# p对，是这个。版主大大能否给出具体步骤？？？

因为有内切圆的等腰梯形的腰的长度等于上下底长度和的一半，所以我把上底复制到左下与下底连到一起，见左下蓝色直线，以得到上下底的长度和。然后以上下底的长度之和为直径，用两点画圆方法画了右边的红色大圆，然后以其圆心为基点移动到梯形左下角（即左边红色大圆，为了看得清楚，右边的红色大圆我没删）。因为这个圆的半径是梯形上下底长度和的一半，也就是等腰梯形腰的长度，等腰梯形上底的左端点必然在这个圆上。然后以上底中点为基点，复制上底到下底中点，再以其左端点为基点，向上移动它到和左边红色大圆的递延交点，从而得到了等腰梯形。接下来画其内切圆……
! H/ p: w$ a& F! n0 J5 H1 E$ A

明天你好吗

woaishuijia 发表于 2016-1-29 20:33
7 Y2 y& E$ v- \0 |因为有内切圆的等腰梯形的腰的长度等于上下底长度和的一半，所以我把上底复制到左下与下底连到一起，见左 ...

拜谢，拜谢，终于有统一解了。版主大大要是哪天有不规则四边形的解法，希望分享。再次谢谢