Solid Edge ST5圆心特征在圆中的矩形阵列

大有茗堂

Solid Edge ST5圆心特征在圆中的矩形阵列
. x$ v$ T: G$ l8 {
圆柱中心有个孔，现需要将它在指定范围的圆形内进行阵列。一般朋友只知道圆形阵列才能保持原始孔在中心。
而矩形阵列由于是指定两个角（适合、填充）或一个起始角（固定）来定矩形的范围的，要想经过原始特征位置上的阵列特征刚好与它重合就得经过计算了。
1.阵列出来的孔规定个数（X向*Y向）。设置为单数。
2.阵列的间距定死。
不同要求在操作时会有些许变化。
关键就在于找出阵列起始点的位置
假设要在直径100的圆内以XY向都间距为9来进行矩形阵列。
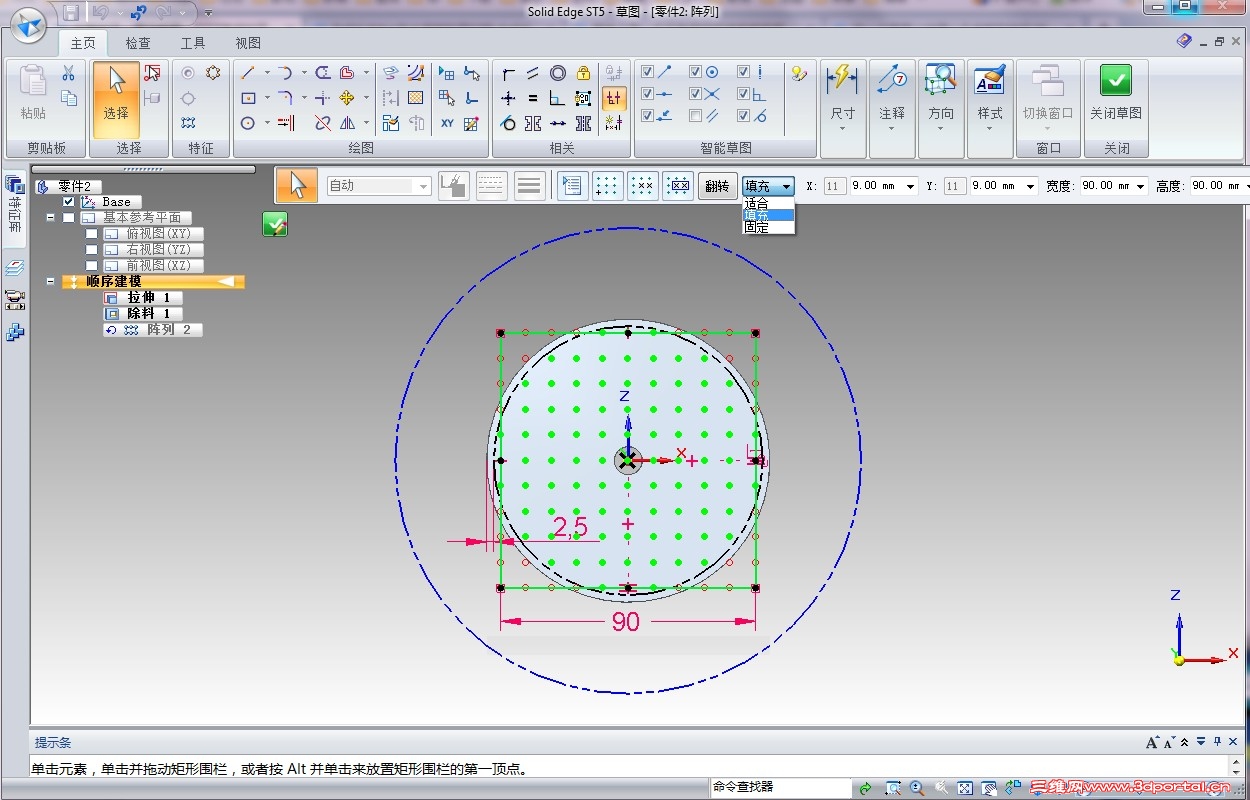
首先画一个辅助正方形，先算最大处能放几个，直径100/间距9＝11，能放11个，那么范围宽就是（个数11-1）*9＝90。所以画一个90宽的正方形。
  P# [) l$ c+ q- L然后以正方形的一个角作为阵列起始点，
阵列类型选择“固定”，然后在X和Y中各输入阵列个数为11间距为9。这样就行了。
# q; Y; b5 t" j9 \' e也可以直接以辅助正方形作为阵列范围（就是直接点正方形的两个对角点来确定阵列范围）这样比较省事。
% e0 {8 }9 E8 R7 c1.阵列类型选择“填充”，X和Y间距各为9。
2.也可以类型选择“适合”，X和Y个数各为11。
1 T% }4 m4 ~4 U7 f
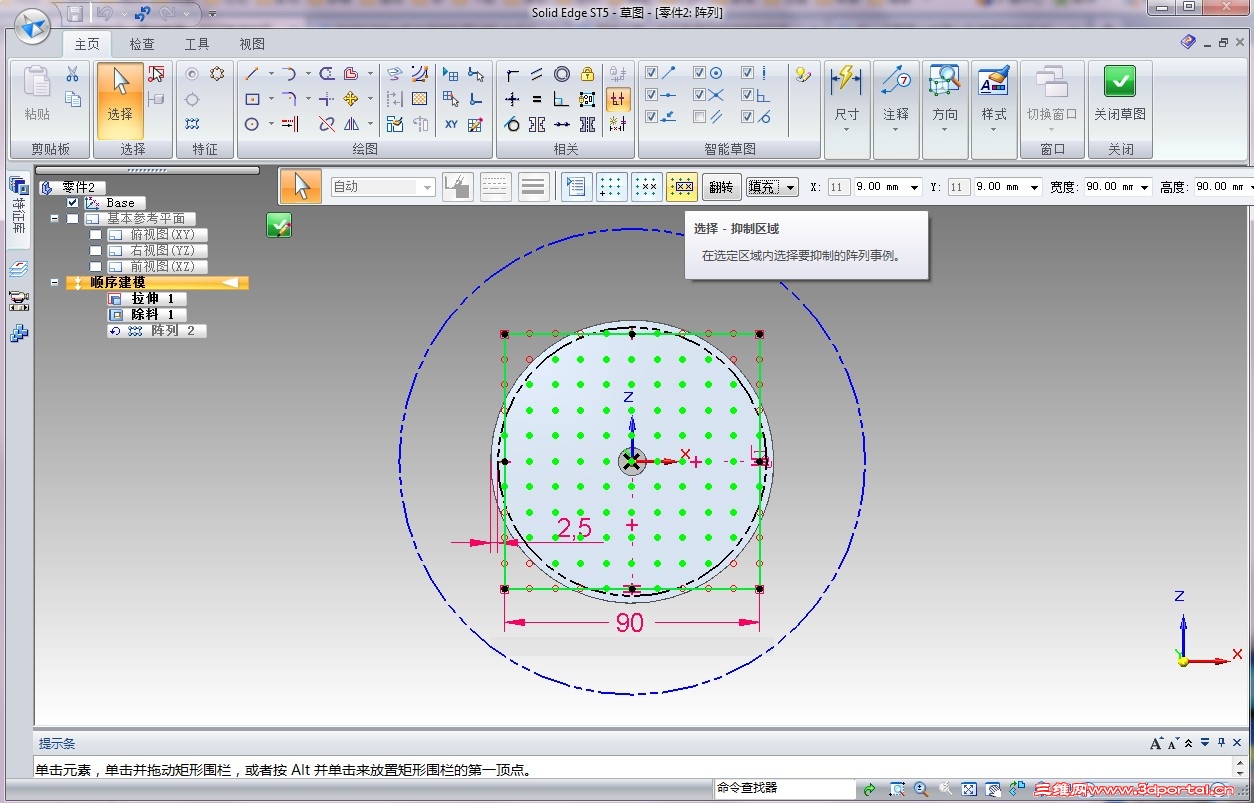
由于是矩形阵列，所以会有一些阵列特征处于指定的圆以外，也有一些虽在圆内，但由于过于靠近边界，也无法形成完整特征，所以都得抑制掉。可以一个个点来抑制，也可以快速抑制，绘制一个大圆所这些特征全包在内，然后再以圆的边界包含并偏置0.5特征直径（直径针对圆，要是其它特征时就选择该特征最大尺寸）绘制小圆，然后用“抑制区域”来分别选择这两个大、小圆，就可以快速把这些不需要的阵列特征全抑制掉了。
. T4 P" O; h6 ~! `8 y, K
5 W+ [+ @! J4 Y5 _& o) T" x  \

: E, u. T6 Q' L, M- O/ k9 S
, n. [5 N; A: s; u2 Y
/ i* d1 D" Z0 H- J* }7 F1 j, d4 \

8 a0 E  {3 o5 n
  q  R1 ~& u9 F+ w8 c

大有茗堂

上传视频附件1-2

大有茗堂

上传视频附件3-4

大有茗堂

上传视频附件5-6