|
根据简谐振动规律,' g% L: C, k1 V( F5 b5 B, z
主轴轴心O1径向跳动的数学表达式为:
; q8 v* X- ]5 r" H5 h8 Z
 (1)
(1)
( m1 S: s4 x. C0 A式中:φ为主轴的转角:φ= ωt:AY、AZ是轴心分别在Y、Z两个坐标方向上简谐振动的幅值。$ y4 i8 R& H X3 K
: e v7 A: X/ R, [
7 x4 B+ O K# R: r2 o; ?
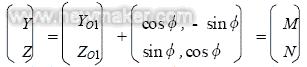 (2)
(2)
1 C4 S1 V; ]# H. B! F* \
* O) r( v) }) \5 p
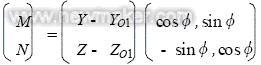 (3)
(3)
% d! G" {: ]9 a* |% q6 Y3 s7 S3 主轴纯径向跳动对零件加工的影响
, G' y7 a- \- [& z: J4 ^, d1) 对镗削加工的影响
0 k& [. a" R }% s5 `在镗床上镗孔时,镗刀随镗床主轴一起作旋转运动。当主轴作纯径向跳动时,将使轴心线沿某一固定方向作简谐运动。镗出的孔形是由惯性坐标系中镗刀刀尖的运动轨迹所决定。设镗刀刀尖在动坐标系的位置为:M=R,N=0,其中R为所加工孔的半径。如图6所示。
1 A5 p, V1 y, T x6 s

3 D( f( |# _& d7 F( D" v1 b图6 镗削加工示意图
# z! c' p' c# ?' F4 U将刀具的位置坐标和式(1) 代入式(2) ,
- t+ A* j) O' B可得在惯性坐标系中镗刀刀尖的轨迹参数方程:, q: g3 Z9 x! L( b, _# P
E# b3 e3 ~# g5 s6 S- y
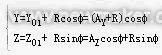 (4)
(4) % Z s6 i( ?+ L7 t- o4 ?! ~* o
将(4) 式平方后整理得:: j& a3 F9 A0 _- {1 |; I% ` {
0 @) \: |0 V/ T0 `
% d3 {* {) I- U( I- [
 (5)
(5) 4 {7 W# X& p. M: x% J- K
(5)式为椭圆的参数方程,其长轴和短轴之半分别为R+AY和R+AYctgφ。因此,在镗孔过程中,主轴有纯径向跳动误差时,那么镗出的孔将是椭圆形的,产生的误差为圆度误差,其值为:△=AY+AZ , V7 H) u4 o# y) l8 y* q
2) 对车削加工的影响4 |2 Z4 u7 p2 Q: A# t, T6 |6 o. E
在车床上加工外圆或镗孔时,工件随车床主轴一起作旋转运动。因此工件被加工表面的几何形状是由刀具在动坐标系中的相对轨迹决定的。设车刀刀尖在惯性坐标系中的坐标位置为Z=0,Y=-R。其中, R为加工半径,如图7所示。 + h4 H1 C* | S- B
 . [+ o0 m. C% C6 @* N# T
. [+ o0 m. C% C6 @* N# T 0 T, T" l! H( c: [( P' ^3 B6 z) J
图7 车削加工示意图 + }: ]: |: q) ^4 U
将刀具的位置坐标和式(1)代入式(3),: V6 w: b) R! A( d0 I" M1 _0 k) R
可得刀具在动坐标系中的轨迹参数方程:( c2 t! i8 C8 [" _5 |
# Q1 X5 @) U+ A+ i5 R2 w
- i5 C2 ?! Q0 q. `
 (6)
(6) 5 ]2 {( e8 y$ g/ z0 ]. h
由式(6) 可得工件被加工表面几何形状的瞬时曲率半径为:. O# V* H0 l- K" F$ z7 M. [
' H0 j8 S+ A7 }8 Y1 E
) O9 H4 j7 c, t5 y) r
 (7)
(7)
# A* ]/ G G8 l# a8 P/ F# N由于幅值AZ的数值很小,可以略去,则式(7) 成为:2 n0 @- E& c5 O9 m1 y E% {2 W
; h Q) I" r5 B q3 e
" e7 [1 s/ H p: A0 a: j% L7 ^8 t, D
 (8)
(8) . Q: [1 |( b! p& r1 U2 M5 R) ^
由式(8)可知,工件横截面的几何形状近似于一个心脏线图形。如图8 所示。
- H. g g" N* E
+ ^( r& L+ T& Z- B. h* ?8 D

# d. h2 }; ^" ?; ]图8 车削加工心形线图
* I W- H& T3 s' @若取ρ1=R-Acosφ,ρ2=R-Acos(p+φ),则D=ρ1+ρ2=2R,( |' M7 l X8 T1 M2 q- y
说明此心脏线是一等径曲线,即工件的横截面几何形状无直径误差。 U" i+ \6 |# N5 X( ]3 `' o) j
当φ=0时,ρ=R-A,当φ=π时,ρ=R+A。所以O1不是加工后工件端面的实际轮廓的中心,工件的实际轮廊中心与O1的距离为A。
: w# l( Z3 B9 H因此可以得出结论:在车床上进行内外圆车削,主轴径向跳动主要影响加工件的同轴度误差,对工件圆度误差的影响可以忽略不计。
( u3 o- Q& x) ~! q' @4 结论; Y* D. }+ W& y/ [( Q6 w7 _* D
通过对主轴纯径向跳动的分析可以看出,主轴回转误差对零件加工精度的影响很大。因此在机械加工中,应采取有效措施减少主轴回转误差对零件加工精度的影响。采取的措施可以从两个方面来考虑。首先要提高主轴的回转精度。主轴轴承是影响主轴回转精度的关键零件,对于精密机床可采用精密的滚动轴承,也采用多油楔动压轴承和静压轴承。同时还要提高与轴承相配合零件的精度。其次要减少主轴回转误差对零件加工的影响。可以采用运动和定位分离的主轴结构,使工件在加工过程中的回转精度不受机床主轴回转误差的影响,使主轴回转误差不反映到工件上。
, f0 U. C Y0 ?# k& v4 W1 q
2 ?' B( V" R) q7 p/ X" D[ 本帖最后由 3dportalzhao 于 2009-5-20 15:26 编辑 ] |