|
|
马上注册,结识高手,享用更多资源,轻松玩转三维网社区。
您需要 登录 才可以下载或查看,没有帐号?注册

x
由于最近较忙,很少来此板块做题,但自己出的题目还是应该给朋友们一个交待,来得晚了,希见谅。
6 ]1 p4 r' F3 S 题目之所以要求不用方程式,并非故弄玄虚,实是SW在阵列过程中方程式是不起作用的,为了公平起见,所以要求不使用方程式。
) j; s% e4 \. R4 b) k 看了几个朋友的答题,确实都能达到总面积相等的要求,都是不错的。在这里我还想提一个进一步的要求,因为我们之所以用阵列,就是当实例数量很大时也能够用阵列的方法得到满意的结果,所以在本题的答案中有的最后用切除切去多余的部分,有的用样条曲线实现面积相等,事实上这些做法虽然阵列出了5个实例,但是在过程中还是需要对每个实例进行个别处理,如正确的切除位置,样条曲线的形状等,如果阵列数很大,恐怕就很麻烦了。
" c! K* j6 h( T7 Z% ]% D4 L( [: w4 w) {. e5 t3 Y6 O: r
我的基本思路是:
?/ k" J, I. }1、 用草图来实现函数运算,自动在阵列过程中根据圆饼的半径(已知条件)求出各圆饼的厚度。" {8 I8 h% O4 L9 L) c, @& B4 `
2、 由于在SW中不支持分离的特征阵列和不支持实体的随形阵列,所以在阵列时先生成一个单实体,然后不需要对每个实例进行后处理的适当办法将单实体转化为多实体。
* s6 N* m* A/ Q* n, t- t, G
' R( y s8 E& o% |6 H M# u模型说明:# C# u; h# \, j, b' G- m
1、 如何实现多实体
2 ?$ _: M% a) m. X8 d, ?1 Y" l5 S2 S) p 在下面动画中“实体-移动/复制1”特征只是将“拉伸1”生成的大圆柱体(实体1)在原位置复制出一个同样的实体(实体2)来。
, J. G" Y7 h9 g( [ “切除-旋转1”特征是用来在实体2种切出一个圆饼的空腔,通过“阵列(线性)1”特征阵列出其它圆饼的空腔。
2 ]" I' r& i! \9 z 最后将二个实体作“组合”(做减法),生成多实体。( \9 Z7 r* I4 M" N/ H2 x5 |
# v) o+ H0 @4 Q
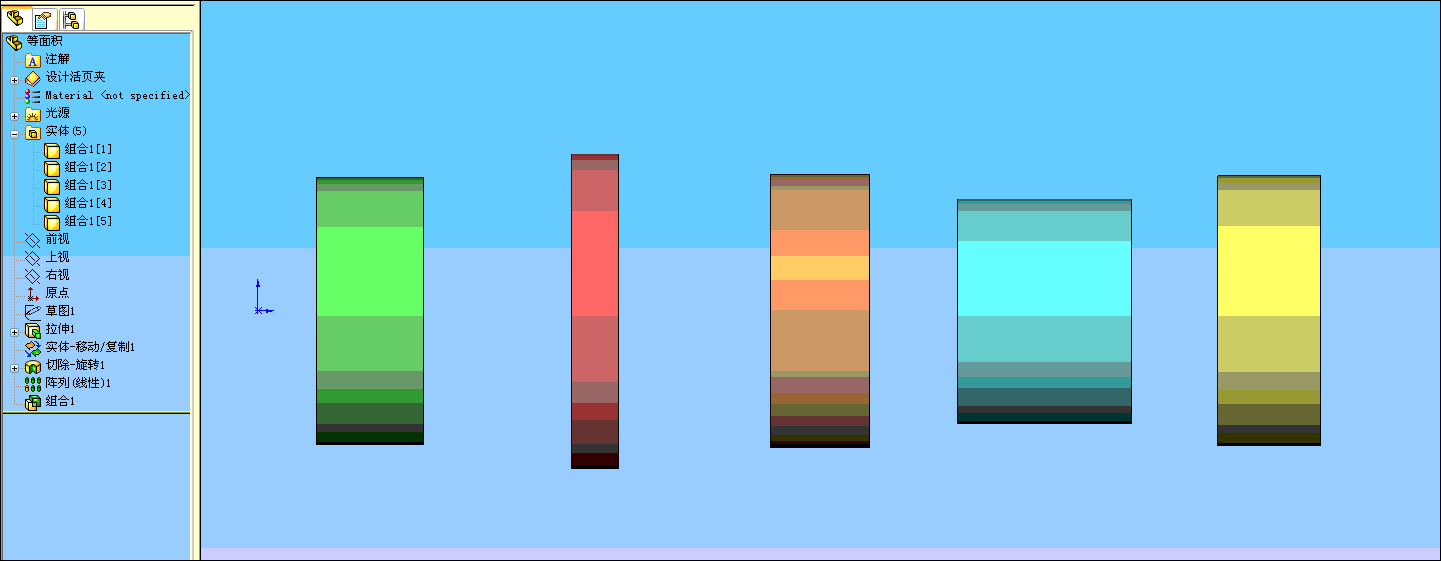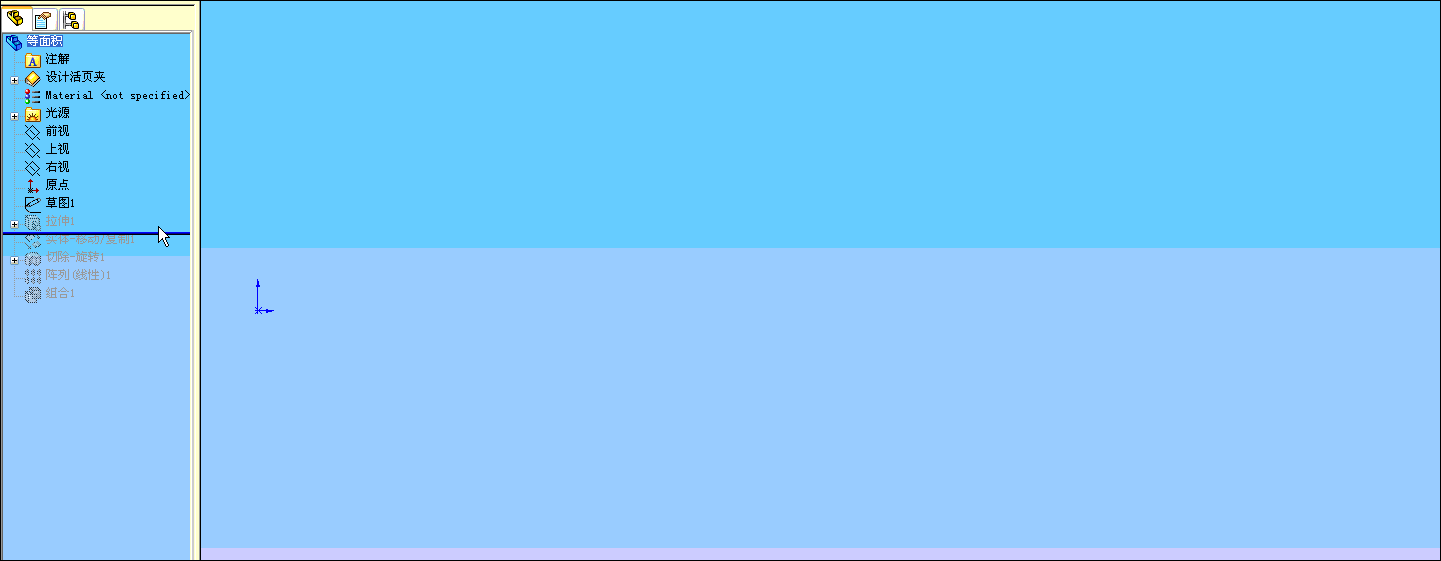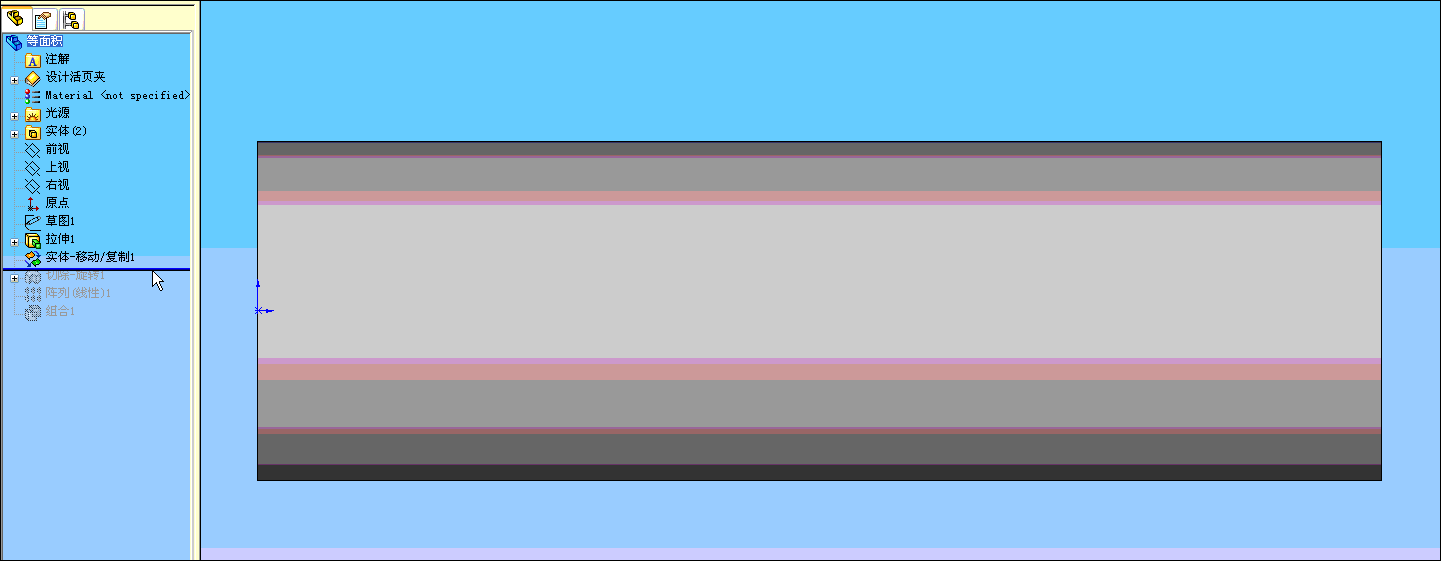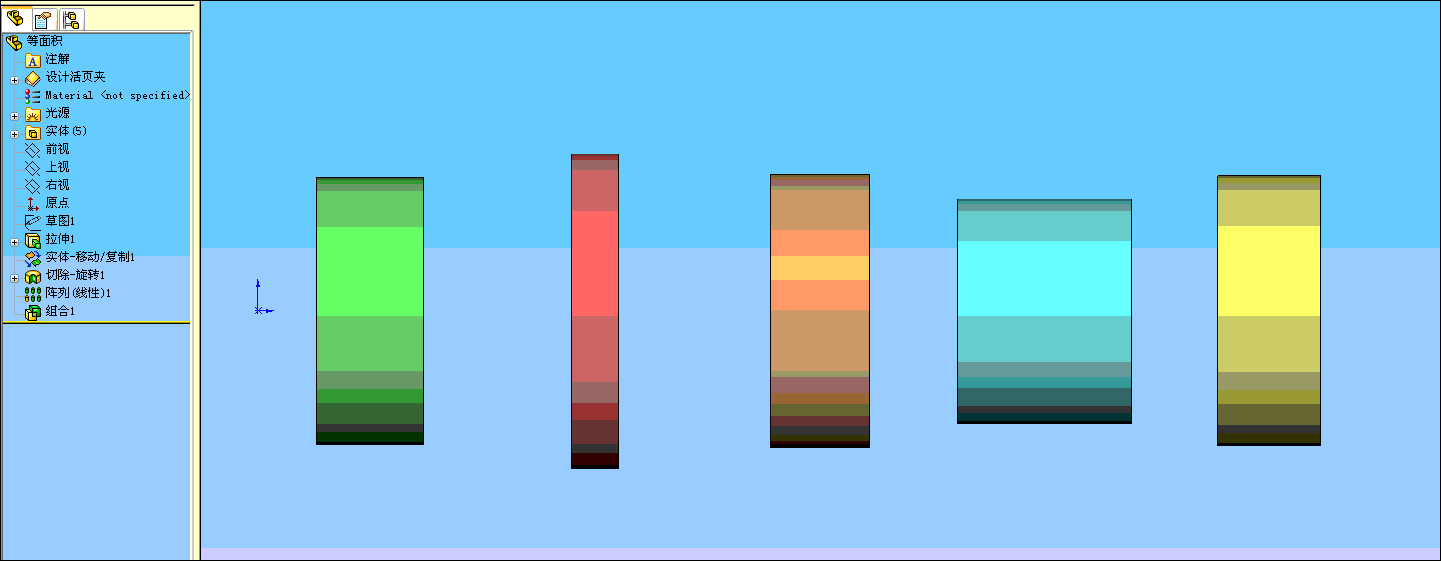 4 A6 S. Q" B, n
4 A6 S. Q" B, n
5 ~. M; W8 f6 N) D1 A" f7 Z- s7 \
当然,实现多实体的方法有多种,个人可以有自己的方法。
: m% s- @5 g8 F1 Q5 ~9 F7 a& k. F
2、 如何实现等面积
* a" O) d' `6 E5 A1 c: p+ T. q, N, m 圆饼的全面积为
; [$ B# B; k3 X2 R/ Q" d 2πr^2+2πrh=2πr(h+r)% c. H) y" K/ c8 t% a- d
按要求此值应等于10000
, T3 W' _# X! Z3 ~# N; ] 故 r(h+r)=10000/(2π)=k^2 ]$ S1 ^# @, I) b, |
其中k为常数, k=100/(2π)^0.5
0 Z7 b9 f5 l3 Z8 U9 i1 X
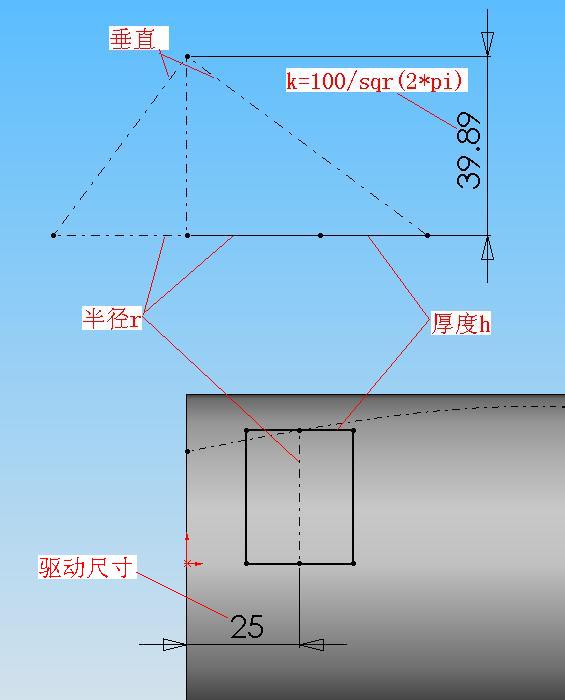
# s# [3 E e+ r' F 在草图中建立一个草图计算块(见图),从草图块中看出符合 r(r+h)=k^2 的要求。用设置几何关系来保证图中的垂直、相等等关系。其中 k 尺寸的输入不能直接输入数值,必须在尺寸输入栏中用输入表达式 100/sqr(2*pi) ,以避免误差,保证总面积尺寸的正确。/ F( j p1 j* G/ K h
- K: P7 X! Q6 h) H# [7 L
# w. ]( _! C# i. s
/ F& |4 X# a5 e 图中尺寸 25 是随形阵列驱动尺寸。显然随着驱动尺寸的增大,半径r也随样条曲线的控制而变化,从而通过草图计算块的计算,使厚度h也作出相应的变化。 |
评分
-
查看全部评分
|