|
|
 发表于 2016-11-15 17:13:47
|
显示全部楼层
发表于 2016-11-15 17:13:47
|
显示全部楼层
来自: 中国天津
本帖最后由 2005llnn 于 2016-11-20 15:29 编辑 * a+ E Q `, t- q
+ z# a; e! v% G2 k7 b c1 v# c没有其他约束条件,此题多解。(线段HG=HE? 眼就是尺啊!)
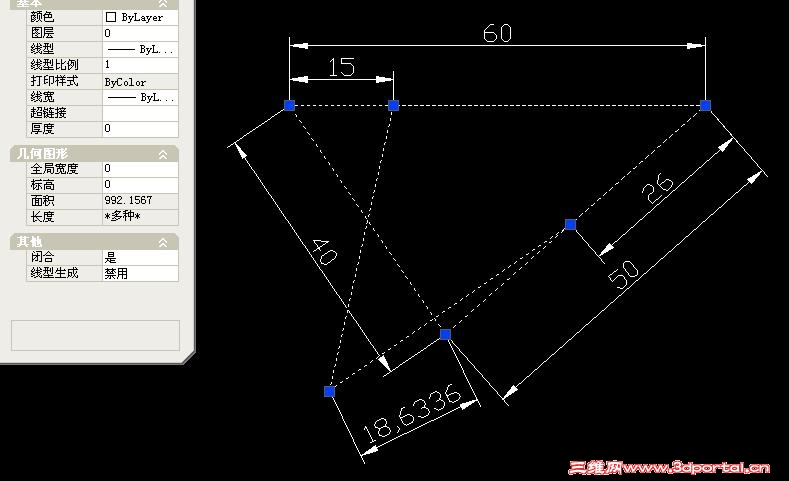
' `' ]: U: x \7 h" L
/ v" P! m8 r- H3 n, I, p# e# Y9 j / c; R- h; L& r: a1 U8 K* ?2 V
7 }7 K7 q& B. E u/ h; C+ y
3 A, t7 x* Q6 T1 x3 }: u9 n
/ e! E* n6 k/ _8 S0 t
5 q+ s4 E. w( n- d; g5 y% v |
评分
-
查看全部评分
|