正弦交流电路相量法悬赏求助50三维币

江浩南

正弦交流电路相量法悬赏求助50三维币
问题很简单，谁能把下面这个图的原理讲的简单易懂，我就奖给他50三维币

ramberer

左图相量A是一旋转有向线段，它的初始位置（t＝0时的位置）与横轴正方向的夹角等于正弦量的初相位φ，并且以正弦量的角频率ω作逆时针方向旋转。在直角坐标系中。有向线段的长度代表正弦量的幅值Um，
: a( q4 Z% |9 z右图曲线正弦量在某时刻的瞬时值就可以由这个旋转有向线段于该瞬时在纵轴上的投影表示出来。这一旋转有向线段具有正弦量的三个特征，故可用来表示正弦量。
表示正弦量的复数称为相量，并在大写字母上打“.” 。相量只是表示正弦量，不是等于正弦量。

CLIMBER7112

4 }' \$ K2 n* {9 T& y; @" g
% y  d( i! R1 E/ Q' j; {2#对楼主的问题作了较正式的讲解，但我猜测楼主的理解难点在于对“正弦量的初相Ψ与复数A的幅角相对应”这一点。我来帮楼主做一下浅显一点的解释：根据复数的概念，复数是由实数和虚数两部分组成，可以由在以实轴和虚轴所组成的坐标系的有向线段表示，有向线段的长度为复数的模，该有向线段与实轴的角度为复数的幅角，该有向线段在实轴上的投影即为复数的实数部分（其值为模与幅角余弦的乘积，称余弦量），有向线段在虚轴上的投影即为复数的虚数部分（其值为模与幅角正弦的乘积，称正弦量）。根据坐标系的灵活建立，任何一个复数都可以加以演化成一个纯实数（即余弦量）或一个纯虚数（即正弦量），但一旦坐标系建立了，则有向线段的复数表达式（即实数部分和虚数部分也就确定了）。根据交流电的产生原理，交流电的最大值是由磁场中转子的大小和磁场的强度决定的，是一个事先就可以确定的值，而交流电的瞬时值却是依转子与磁力线的切割角度成正弦函数变化的，由于转子的角速度ω可事先确定，则转子与磁力线的切割角度只是随时间变化而变化。基于这一规律，电子工程上，为了描述和计算方便，引入复数A的正弦量来表示正弦交流电，交流电的最大值对应复数A的模值，正弦交流电瞬值的变化即对应于复数的正弦量因其幅角随时间变化而相应变化，即正弦量的角频率即对应复数A（有向线段）绕轴旋转的角速度，正弦量三角函数中的变量(ωt+Ψ)统称正弦量的相位，当t=0时（即初始时），此时，正弦量的相就是初相，当然也就是Ψ。当正弦量的瞬值为零时，即ωt+Ψ=0，即ωt=-Ψ，也就是说，右图的函数曲线交ωt轴于（-Ψ，0）点。由于它位于坐标原点的左边，而ω一定，则时间t为一个负值，这就相当于时光倒流，这时对应于复数A亦随着倒流的时间t转动一个等于其幅角Ψ的角度回到正弦量为零的位置，而这个角度Ψ本来就是复数A幅角的初始值Ψ（有向线段与实轴的初始角），显而易见“正弦量的初相Ψ是与复数A的幅角的初始值Ψ相对应的"
8 M$ ?9 q5 o% q. W/ [$ |
6 b1 r  |7 F2 k0 h! O  r. V反过来，也就不难理解为什么对应到上边所说的或者楼主所给出的右图中的Ψ人们称之为正弦量的初相了（理由很简单，无外乎便于对应而已）。
. i( R% `! z; r7 j0 f    不知这样解释，楼主是否懂了呢？

燕赵之鹰

1、时间一一对应关系
# E1 W+ {9 D7 j2、幅值一一对应关系
. j3 [: r* o: }6 g9 G) _7 @6 d5 x3、匀角速度旋转
4、时间轴匀速展开
1 ~" N4 {# }$ @$ E8 v5 J  U% Q! k7 e5 N5、找到对应点是理解问题的关键，而且需要动态理解

cylzwx

( s3 S8 C* j6 k: \9 o
相量法:
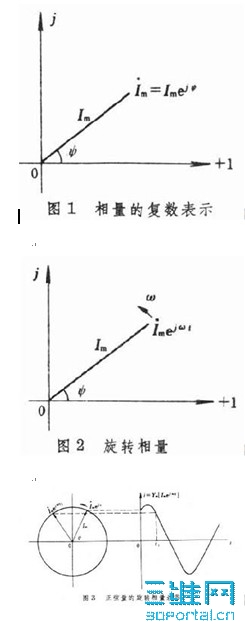
相量图 　相量是一个复数，复数在复平面上可以用一个矢量来表示，所以一个相量可以用复平面上的一个矢量来表示,如图1所示。这种表示相量的图称为相量图。若相量乘上ejwt,则表示该相量的矢量以角速度ω绕原点反时针旋转，于是得到一个旋转矢量,如图2所示。这个旋转矢量称为旋转相量，它在任何时刻在虚轴上的投影即为正弦量在该时刻的瞬时值，如图3所示。


　　引入相量后，两个同频正弦量的加、减运算可以转化为两个相应的相量的加、减运算，相量的加减运算既可通过复数运算进行，也可在相量图上按矢量加、减法则进行。另外，常遇到的正弦量乘以任意实常数和正弦量对时间求导数的运算可分别转化为正弦量的相量乘以该任意实常数和正弦量的相量乘以的jω 运算。

fieldf

这个很好理解呀,右图的正弦波形,就是左图A点随时间运动后的投影轨迹.因为起始点的不同,自然就有初相了.楼主觉得这样解释够简单吗?

tangshan

这个问题好像不是很难，你的那张图说的很清楚了

郝工在线

找本电工学苦读一下，问题就迎刃而解了

cspc103

楼主 相量的引入是一种数学变换 不能以矢量来看 楼主要好好学习一下 电路或电工的相关章节才能明白 三言两语说不清楚

ysjd2001

正弦有三要素,三要素就确定正弦量.现在用圆半径代表最大值.旋转速度代表角频率.向量角代表初相位,简单的说机最大直向量