|
|
马上注册，结识高手，享用更多资源，轻松玩转三维网社区。
您需要 登录 才可以下载或查看，没有帐号？注册
x
与老美工程师关于CPk的一次PK& S) ?' E0 J1 ^
我公司长期与美方一家公司提供产品，美方是一家全球500强的企业，对产品质量的要求自然非常严格，经常要求我们提供产品CPk分析报告。接到我们的报告后，通常用minitab进行CPk计算。今年又一次我们提交了一个新产品平面度的测试数据。没几天对方来信说不合格，我把数据又认真地看了看，(数据如下，平面度公差：不大于0.5)
9 s X1 S+ K# \- v5 Z: p0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.11,0.12,0.13,0.14,0.14,0.15,0.15,0.15,0.16,0.17,0.17,0.17,0.18,0.2,0.21,0.21,0.21,0.22,0.22,0.22,0.23。* ~9 _5 a; `0 b. l+ B! Y/ @3 O
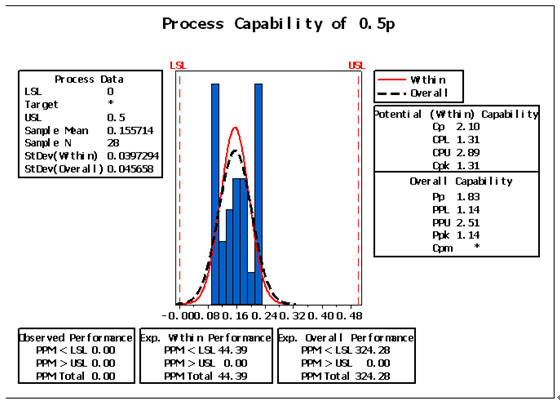
数据没有超差的。于是请美方把不合格的理由详细说明一下，美方工程师把他用MINITAB 作的CPk图表传了过来，如图：$ {! D: F; |$ O4 B- X# _6 _
0 n- L" k8 r" q9 O/ [. Y; M理由是数据没有正态分布，两侧出现两个峰值。! }2 p0 L# j5 A8 d! T7 g M
应该说，从图上看老美工程师说得有道理。但我对数据背景情况非常清楚，于是我回答了以下几点
' D* P% C( y3 b8 s1、3 `' H2 o0 Q( F! @9 N, Q) z
MINITAB软件在分析CPK时，要求把数据分组，由于样本数量少，分组如果过大，就会出现如上图那样的“异常”，影响判断。本例中，0.1区段有7个数据，而在0.21和0.22 区段各有3个数据，0.23有1个数据，MINITAB 把后面的7个数据归为一组，这样得出的数据变成两边高中间低的形态了。如果根据数据分布用EXCEL做出柱壮图来看，形态就完全两样。 F3 R+ `' s" u7 }
2、
) W: \6 r* R0 a3 g2 z0 k由于处于新产品试制过程，样本量很小，只有28个，用来证明是否正态是不够的；# g' @* g4 ]9 b$ O1 J, h; r
3、
% T. G. _- r' U7 B+ [/ c平面度是一种单边公差，而对方的分析基点仍然是双向公差，以此计算的CPk有错；- V- ~2 O/ n. P0 |1 k" s7 }
老美工程师在接到我的答复后，很正式地来函认可我的意见，一切OK。 |
-
评分
-
查看全部评分
|
发表于 2009-9-6 12:48:57
发表于 2009-9-9 16:29:56
楼主
