|
|
马上注册,结识高手,享用更多资源,轻松玩转三维网社区。
您需要 登录 才可以下载或查看,没有帐号?注册

x
摘要:在用SPC进行质量控制的过程中, 其核心是对产品进行合理分组抽样后, 再进行的质量特性数据的分析.正态分布已经贯穿整个质量特性数据分析的过程, 是进行质量控制的最重要的工具. 3 f7 r+ u9 t; H' c- `
( @ J M- g; L: A. z
正态分布
- x( Z$ D5 Q9 P" {: Q正态分布是指变量的频数或频率呈中间最多,两端 逐渐对称地减少,表现为钟形的一种概率分布。从理论上说,若随机变量x的概率密度函数为:
, a7 s m. s# Y- X3 o

+ H, S9 u0 [9 N8 r5 c则称x服从均数为μ,标准差为σ2的正态分布。
3 v' {+ o6 M) D2 \! [# @. ]$ j' M! s* z) C+ w2 Q2 O2 R
正态分布的特点
" ?3 m( \1 x' t1 o; ?•正态分布有两个参数(parameter),即位置参数(均数)和变异度参数(标准差)。
$ O% C% t! i9 g•高峰在均数处;
6 A6 F1 N- |# c& J•均数两侧完全对称。 : I8 Z- V, O8 Q, K7 z: [
•正态曲线下的面积分布有一定的规律。. [ n! ^% G' a( U5 _# }- f
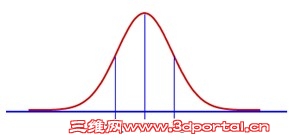
$ P1 m8 [7 D5 E L% c•X轴与正态曲线所夹面积恒等于1 。- R( x* v9 ~* E8 m4 f, {" |
•对称区域面积相等。
8 y+ F [4 [. w' m w
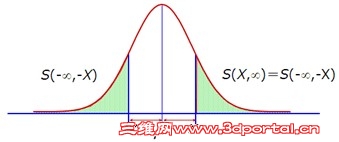
: w" r! q# T! t* ~2 [1 b正态曲线下面积的分布规律/ G3 m8 b! E; j6 t( _
•正态曲线下面积的意义:正态曲线下一定区间内的面积代表变量值落在该区间的概率。整个曲线下的面积为1,代表总概率为1。
) a! C0 f6 s- w' \, S! }; n. ~•曲线下面积的求法:定积分法和标准正态分布法- K2 A9 n& ^) o9 j9 y8 ~$ j0 k
; |; Q: _0 l# v" j
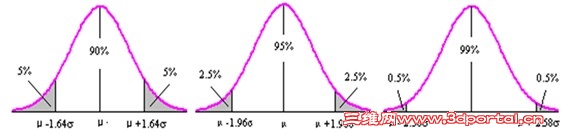
正态分布曲线下的面积
3 r& b7 P3 b& U•μ±σ范围内的面积为68.27%2 k9 c1 X0 E n% E" o& \4 b Z
•μ±1.96σ范围内的面积为95%! W5 L" ]- o0 j
•μ±2.58σ范围内的面积占99%) Q u4 F% n% N7 e% X1 r9 s2 [
 2 ?! l+ C9 a- x0 W% n: y% H7 Y
2 ?! l+ C9 a- x0 W% n: y% H7 Y
正态分布在质量控制中的意义
5 I/ p! _- i b! Y& y" M$ X/ n# x 当我们运用正态分布曲线、直方图、控制图等工具对质量特性数据进行分析和控制时,正态分布是其中最为关键的工具,因为在正常情况下产品质量特性值的分布,一般都服从正态分布或近似正态分布;并且在控制图的使用上,也要求抽样数据符合正态分布作为前提;在最后进行的过程能力分析时也必须符合先要达到正态分布这个条件.所以正态分布已经贯穿整个质量特性数据分析的过程.! S- K) x/ r% q0 |) g# O7 M
符合正态分布的事物在日常生活中是普遍存在的,它具有一定的广泛性.正态分布在对产品的质量特性数据的分析过程中占有重要的地位.在运用正态分布检验质量特性时,可以以它为基础,并在此基础上构筑出高效实用的检验方法和检验步骤,这为SPC的发展和应用打下了坚实的基础.
7 [0 V% ?( d" X4 t; @- A
" H2 U" }0 F' M+ I& |4 s附:SPC质量控制分析软件免费下载地址:http://www.gztaiyou.com/Download/Try.html
" [1 V2 J F+ }# ^# [/ P* }; u' o( ~" `( I
N6 ?8 c2 u. C. Z, W
|
|